-
PDF
- Split View
-
Views
-
Cite
Cite
Tomoaki Ishiyama, Francisco Prada, Anatoly A Klypin, Manodeep Sinha, R Benton Metcalf, Eric Jullo, Bruno Altieri, Sofía A Cora, Darren Croton, Sylvain de la Torre, David E Millán-Calero, Taira Oogi, José Ruedas, Cristian A Vega-Martínez, The Uchuu simulations: Data Release 1 and dark matter halo concentrations, Monthly Notices of the Royal Astronomical Society, Volume 506, Issue 3, September 2021, Pages 4210–4231, https://doi.org/10.1093/mnras/stab1755
Close - Share Icon Share
ABSTRACT
We introduce the Uchuu suite of large high-resolution cosmological N-body simulations. The largest simulation, named Uchuu, consists of 2.1 trillion (12 8003) dark matter particles in a box of side-length 2.0 |$\, h^{-1} \, \rm Gpc$|, with particle mass of 3.27 × 108|$\, h^{-1}\, \rm M_{\odot }$|. The highest resolution simulation, Shin-Uchuu, consists of 262 billion (64003) particles in a box of side-length 140 |$\, h^{-1} \, \rm Mpc$|, with particle mass of 8.97 × 105|$\, h^{-1}\, \rm M_{\odot }$|. Combining these simulations, we can follow the evolution of dark matter haloes and subhaloes spanning those hosting dwarf galaxies to massive galaxy clusters across an unprecedented volume. In this first paper, we present basic statistics, dark matter power spectra, and the halo and subhalo mass functions, which demonstrate the wide dynamic range and superb statistics of the Uchuu suite. From an analysis of the evolution of the power spectra, we conclude that our simulations remain accurate from the baryon acoustic oscillation scale down to the very small. We also provide parameters of a mass–concentration model, which describes the evolution of halo concentration and reproduces our simulation data to within 5 per cent for haloes with masses spanning nearly eight orders of magnitude at redshift 0 ≤ z ≤ 14. There is an upturn in the mass–concentration relation for the population of all haloes and of relaxed haloes at z ≳ 0.5, whereas no upturn is detected at z < 0.5. We make publicly available various N-body products as part of Uchuu Data Release 1 on the Skies & Universes site.1 Future releases will include gravitational lensing maps and mock galaxy, X-ray cluster, and active galactic nucleus catalogues.
1 INTRODUCTION
Over the last three decades, our knowledge of the formation of structure in the Universe and its growth has been dramatically advancing. The lambda cold dark matter (ΛCDM) paradigm is now regarded as the standard model to describe our Universe, in which structure formation occurs hierarchically. Smaller scale structures gravitationally collapse first and form dark matter haloes, which repeats with time to produce larger and larger scale structures.
Luminous objects, such as galaxies and active galactic nuclei (AGNs), form in the centres of haloes and trace this growth in structure. From their light, we can extract valuable information about the underlying cosmology. The properties of galaxies and AGNs at various epochs also contain information that reveals the physics of their formation. Ongoing/upcoming wide and deep photometric/spectroscopic surveys performed by the Subaru Hyper Suprime-Cam (HSC: Miyazaki et al. 2006, 2012), the Subaru Prime Focus Spectrograph (PFS: Takada et al. 2014), and Euclid (Laureijs et al. 2011), amongst others, will offer vast amounts of data on galaxies and AGNs, covering many Gpc in scale. This data revolution is driving our understanding of the Universe to unprecedented detail. However to be successful, such experiments require per cent-level precision theoretical predictions in order to quantify potential deviations from ΛCDM, to separate out cosmological from baryonic effects, and to identify other sources of systematic error.
To extract as much information as possible from such observations, we need detailed ‘mock’ galaxy and AGN catalogues. Traditionally, dark matter only cosmological N-body simulations have played a central role in this effort, especially when coupled with semi-analytical galaxy formation models (e.g. Benson 2012; Croton et al. 2016; Makiya et al. 2016; Cora et al. 2018; Shirakata et al. 2019). Several catalogues and simulations of this sort are publicly available. These include the Millennium simulation galaxy catalogues (Springel et al. 2005; Croton et al. 2006), galaxies built on the MultiDark simulation (Prada et al. 2012; Klypin et al. 2016; Knebe et al. 2018), as well as ν2GC (Ishiyama et al. 2015; Makiya et al. 2016; see e.g. http://skiesanduniverses.org/ and https://tao.asvo.org.au/).
More recently, galaxy catalogues using cosmological hydrodynamical simulations have become available, such as EAGLE (Schaye et al. 2015), Horizon-AGN (Dubois et al. 2014), Illustris (Vogelsberger et al. 2014; Springel et al. 2018), and Magneticum (Dolag et al. 2015; for a recent review, see Vogelsberger et al. 2020). However, their current simulation size is typically of the order ∼100 |$\, h^{-1} \, \rm Mpc$| in scale, which is much smaller than the observational surveys looking to extract cosmological information. Therefore, large N-body simulations and semi-analytical galaxy formation models remain an essential way to construct appropriate mock catalogues for comparison to the observations.
The challenge lies in producing the most closely matched mock catalogues as possible. For this, the simulation volume must be comparable with those covered by the surveys, and the mass resolution must be sufficient to resolve those galaxies formed in the early Universe that are expected to ultimately feature in the observations. This balance of size and resolution is critical. Nowadays, cosmological N-body simulations with more than 1011 particles have been achieved on large modern supercomputers (e.g. Skillman et al. 2014; Ishiyama et al. 2015; Potter, Stadel & Teyssier 2017; Cheng et al. 2020). However, none of them yet satisfy both requirements simultaneously. For example, the Euclid Flagship simulation (Potter et al. 2017) contains 2 trillion particles over a cosmologically large volume. But to achieve such a volume its mass resolution is ∼109|$\, h^{-1}\, \rm M_{\odot }$|, a high-mass limit in the early Universe where the need is to accurately resolve the progenitor galaxies that will be observed.
There are further complications. Although simulations like the Euclid Flagship simulation leverage the latest supercomputing hardware and algorithms to get ever so closer to producing an ideal mock universe, linking the evolution of the unique structures within across time remains a significant hurdle. This linking takes the form of halo/subhalo merger trees, which are required by modern semi-analytical galaxy models to construct mock catalogues. Without these, simulation teams must rely on empirical models to construct their mock universes, like abundance matching (e.g. Kravtsov et al. 2004; Vale & Ostriker 2004; Conroy, Wechsler & Kravtsov 2006; Shankar et al. 2006; Behroozi, Conroy & Wechsler 2010; Moster et al. 2010; Reddick et al. 2013) and the halo occupation distribution method (e.g. Peacock & Smith 2000; Seljak 2000; Berlind & Weinberg 2002; Cooray & Sheth 2002; Zheng, Coil & Zehavi 2007; Leauthaud et al. 2012). Such mocks thus lack evolutionary information for individual objects (haloes or galaxies), and their use for analysis and interpretation of the observations can be limited. Also, given their statistical nature, empirical models are further removed from the physics of galaxy formation when compared to semi-analytical galaxy formation models.
To address these problems, we have run a suite of ultra-large cosmological N-body simulations, the Uchuu2 simulation suite, on which the halo/subhalo merger trees have been constructed. The largest Uchuu simulation consists of 12 8003 ≈ 2.1 trillion dark matter particles in a box of 2.0 |$\, h^{-1} \, \rm Gpc$| side-length; this results in a mass of each dark matter particle of 3.27 × 108|$\, h^{-1}\, \rm M_{\odot }$|. The highest resolution simulation in the suite consists of 64003 particles in a 140 |$\, h^{-1} \, \rm Mpc$| box, with particle mass of 8.97 × 105|$\, h^{-1}\, \rm M_{\odot }$|. The cosmological parameters for all Uchuu simulations are based on the latest observational results obtained by the Planck satellite (Planck Collaboration VI 2020). Thanks to its large volume and high-mass resolution, our simulation suite provides the most accurate theoretical templates to construct galaxy and AGN catalogues to date.
In this paper, we introduce the Uchuu simulation suite and describe the public release of various N-body dark matter data products. These include subset particles drawn from each simulation, matter power spectra, halo/subhalo catalogues, their merger trees, and various lensing products. These comprise Data Release 1 (DR1). Details of the lensing products are given in a companion paper (Metcalf et al., in preparation). Mock galaxy catalogues constructed using three semi-analytical models – ν2GC (Makiya et al. 2016; Shirakata et al. 2019), SAG (Cora et al. 2018), and SAGE (Croton et al. 2016) – will be released as an official Data Release 2 (DR2) in the near future. All data will be made publicly available on the Skies & Universes site at http://skiesanduniverses.org/.
The current paper is organized as follows: In Section 2, we describe the simulation and numerical methods used to produce the Uchuu data. In Section 3, we present matter power spectra and mass functions as standard validations of our simulations, along with other statistics measured at the unprecedented detail Uchuu affords. To conclude, our work is summarized in Section 4.
2 INITIAL CONDITIONS AND NUMERICAL METHOD
The basic properties of the cosmological N-body simulations that comprise the Uchuu suite are listed in Table 1. The largest simulation, simply named Uchuu, was run using 12 8003 dark matter particles in a comoving box of side-length 2.0 |$\, h^{-1} \, \rm Gpc$|, resulting in a dark matter particle mass resolution of 3.27 × 108|$\, h^{-1}\, \rm M_{\odot }$|. The gravitational softening length of Uchuu is 4.27 |$\, h^{-1} \, \rm kpc$|. We additionally produced two smaller volume simulations that are otherwise identical to the full Uchuu simulation. The first, named mini-Uchuu, was run with 25603 particles in a 400 |$\, h^{-1} \, \rm Mpc$| comoving side-length box. The second, named micro-Uchuu, was run with 6403 particles in a 100 |$\, h^{-1} \, \rm Mpc$| comoving side-length box. These two simulations have a considerably smaller data footprint, and hence act as convenient testing simulations, amongst other applications. Finally, to push the resolution of Uchuu to lower mass haloes, a higher resolution simulation was run, named Shin-Uchuu,3 using 64003 particles. This simulation has a comoving box of side-length 140 |$\, h^{-1} \, \rm Mpc$| and particle mass of 8.97 × 105|$\, h^{-1}\, \rm M_{\odot }$|. Its gravitational softening length is 0.4 |$\, h^{-1} \, \rm kpc$|.
Properties of the cosmological N-body simulation suite presented in this work. Here, N, L, ε, and mp are the total number of particles, box length, softening length, and particle mass resolution, respectively. The first four rows are for the Uchuu suite. The next is the Phi-4096 simulation used to parametrize the mass–concentration relation, as described in Section 3.4. Lastly is the glam simulation used to evaluate cosmic variance on the power spectrum, the details of which are given in Section 3.1.
| Name . | N . | L . | ε . | mp . |
|---|---|---|---|---|
| . | . | (|$\, h^{-1} \, \rm Mpc$|) . | (|$\, h^{-1} \, \rm kpc$|) . | (|$\, h^{-1}\, \rm M_{\odot }$|) . |
| Uchuu | 12 8003 | 2000.0 | 4.27 | 3.27 × 108 |
| Mini-Uchuu | 25603 | 400.0 | 4.27 | 3.27 × 108 |
| Micro-Uchuu | 6403 | 100.0 | 4.27 | 3.27 × 108 |
| Shin-Uchuu | 64003 | 140.0 | 0.4 | 8.97 × 105 |
| Phi-4096 | 40963 | 16.0 | 0.06 | 5.13 × 103 |
| glam | 20003 | 2000.0 | 286 | 8.60 × 1010 |
| Name . | N . | L . | ε . | mp . |
|---|---|---|---|---|
| . | . | (|$\, h^{-1} \, \rm Mpc$|) . | (|$\, h^{-1} \, \rm kpc$|) . | (|$\, h^{-1}\, \rm M_{\odot }$|) . |
| Uchuu | 12 8003 | 2000.0 | 4.27 | 3.27 × 108 |
| Mini-Uchuu | 25603 | 400.0 | 4.27 | 3.27 × 108 |
| Micro-Uchuu | 6403 | 100.0 | 4.27 | 3.27 × 108 |
| Shin-Uchuu | 64003 | 140.0 | 0.4 | 8.97 × 105 |
| Phi-4096 | 40963 | 16.0 | 0.06 | 5.13 × 103 |
| glam | 20003 | 2000.0 | 286 | 8.60 × 1010 |
Properties of the cosmological N-body simulation suite presented in this work. Here, N, L, ε, and mp are the total number of particles, box length, softening length, and particle mass resolution, respectively. The first four rows are for the Uchuu suite. The next is the Phi-4096 simulation used to parametrize the mass–concentration relation, as described in Section 3.4. Lastly is the glam simulation used to evaluate cosmic variance on the power spectrum, the details of which are given in Section 3.1.
| Name . | N . | L . | ε . | mp . |
|---|---|---|---|---|
| . | . | (|$\, h^{-1} \, \rm Mpc$|) . | (|$\, h^{-1} \, \rm kpc$|) . | (|$\, h^{-1}\, \rm M_{\odot }$|) . |
| Uchuu | 12 8003 | 2000.0 | 4.27 | 3.27 × 108 |
| Mini-Uchuu | 25603 | 400.0 | 4.27 | 3.27 × 108 |
| Micro-Uchuu | 6403 | 100.0 | 4.27 | 3.27 × 108 |
| Shin-Uchuu | 64003 | 140.0 | 0.4 | 8.97 × 105 |
| Phi-4096 | 40963 | 16.0 | 0.06 | 5.13 × 103 |
| glam | 20003 | 2000.0 | 286 | 8.60 × 1010 |
| Name . | N . | L . | ε . | mp . |
|---|---|---|---|---|
| . | . | (|$\, h^{-1} \, \rm Mpc$|) . | (|$\, h^{-1} \, \rm kpc$|) . | (|$\, h^{-1}\, \rm M_{\odot }$|) . |
| Uchuu | 12 8003 | 2000.0 | 4.27 | 3.27 × 108 |
| Mini-Uchuu | 25603 | 400.0 | 4.27 | 3.27 × 108 |
| Micro-Uchuu | 6403 | 100.0 | 4.27 | 3.27 × 108 |
| Shin-Uchuu | 64003 | 140.0 | 0.4 | 8.97 × 105 |
| Phi-4096 | 40963 | 16.0 | 0.06 | 5.13 × 103 |
| glam | 20003 | 2000.0 | 286 | 8.60 × 1010 |
To generate the initial conditions for each simulation, we used the parallel 2lptic code4 adopting second-order Lagrangian perturbation theory (Crocce, Pueblas & Scoccimarro 2006). We calculated the matter transfer function using the online version of camb5 (Lewis, Challinor & Lasenby 2000). Throughout, the latest cosmological parameters measured by the Planck Satellite (Planck Collaboration VI 2020) were adopted: Ω0 = 0.3089, Ωb = 0.0486, λ0 = 0.6911, h = 0.6774, ns = 0.9667, and σ8 = 0.8159. The initial redshift for all simulations was 127. The gravitational evolution of each dark matter particle was calculated using the massively parallel treepm code, greem6 (Ishiyama, Fukushige & Makino 2009; Ishiyama, Nitadori & Makino 2012). This was run on the Aterui II supercomputer at the Center for Computational Astrophysics (CfCA), National Astronomical Observatory of Japan, and the K computer at the RIKEN Advanced Institute for Computational Science. The evaluation of the tree forces was accelerated by the phantom-grape7 software (Nitadori, Makino & Hut 2006; Tanikawa et al. 2012, 2013; Yoshikawa & Tanikawa 2018). 50 particle snapshots covering z = 14 to 0 were written to disc.
To identify bound structures within the particle data at each snapshot, the rockstar8 phase space halo/subhalo finder (Behroozi, Wechsler & Wu 2013a) was run. We then constructed merger trees using the consistent trees9 code (Behroozi et al. 2013b). However, by default, consistent trees does not run in parallel in a distributed memory environment. Hence, our use of consistent trees needed to be modified to make merger tree construction possible on simulations of the size of those in the Uchuu suite.
To overcome this hurdle, we split the full box of each simulation into smaller regularly spaced subvolumes, and ran consistent trees for each subvolume separately. In the case of the Uchuu simulation, the rockstar catalogues for each snapshot were broken into 203 subcatalogues of comoving volume 20003/203 = 1003|$(h^{-1} \, \rm Mpc)^3$|. These subcatalogues were then grouped across redshift to construct the merger trees, where subcatalogues in each group occupy the same Euler comoving volume. However, haloes and subhaloes can have progenitor/descendant relationships that lie outside of such defined groups. To account for this, we added haloes and subhaloes to the group if they lay within a 25 |$\, h^{-1} \, \rm Mpc$| distance from any edge of the corresponding Euler volume of the group. However, this also meant that added haloes and subhaloes could be duplicated in multiple groups, and after running consistent trees across all groups, multiple merger tree files constructed separately could have the same trees that contain these overlapping haloes and subhaloes. To correct for this, we ran a final step to clean such overlapping trees from all tree files except for one, thus removing any duplicates. In this way, the merger trees are consistently and efficiently constructed for the entire box. To show the robustness of this method, in Appendix D we compare merger trees from the mini-Uchuu simulation constructed by this method and the original consistent trees code.
In addition to the Uchuu and Shin-Uchuu simulations, we use an additional small volume but ultrahigh resolution simulation, Phi-4096, described in Table 1, focused on z > 7.5. This simulation extends the halo mass range down to 107 |$\rm M_{\odot }$| at high redshift and helps with the evaluation of resolution effects. Phi-4096 is also used when we later examine the halo mass–concentration relation. The cosmological parameters of Phi-4096 are slightly different from those of the Uchuu suite: 1.6 per cent larger for σ8 and less than 1 per cent for the remaining parameters. Dutton & Macciò (2014) show that the average concentration of a halo increases by about 8 per cent when σ8 increases by 7.9 per cent. The latter is much larger than the difference between the Uchuu and the Phi-4096 simulations, and thus we treat all simulations equally in what follows. The initial conditions of Phi-4096 were generated by the publicly available code, music10 (Hahn & Abel 2011). All other numerical tools used to process and study Phi-4096 were the same as those for the Uchuu simulations.
Fig. 1 shows dark matter distribution of the Uchuu simulation at z = 0. The top panel shows a 2000 |$\, h^{-1} \, \rm Mpc$| × 1333 |$\, h^{-1} \, \rm Mpc$| slice of thickness of 25 |$\, h^{-1} \, \rm Mpc$|. To calculate density fields, we used the tetrahedron quadrupole particle mesh (T4PM) method (Hahn, Abel & Kaehler 2013). Vast cosmic web structures are clearly visible. The three bottom panels are close-ups of the largest halo in the box at different zoom levels, highlighting the detail Uchuu can resolve. The mass of this halo is ∼5.0 × 1015|$\, h^{-1}\, \rm M_{\odot }$|. More than a 1000 haloes with mass greater than ∼1.0 × 1015|$\, h^{-1}\, \rm M_{\odot }$| exist in Uchuu, which allows us to study such rare objects with unprecedented statistics. Each such halo is resolved by more than 3 million particles.
Dark matter distribution of the Uchuu simulation at z = 0. The top panel shows a 2000 |$\, h^{-1} \, \rm Mpc$| × 1333 |$\, h^{-1} \, \rm Mpc$| slice of thickness of 25 |$\, h^{-1} \, \rm Mpc$|. The three bottom panels zoom-in on the largest halo in Uchuu, on scales of 250, 38, and 9.4 |$\, h^{-1} \, \rm Mpc$| (moving clockwise). The white box in the top panel is the same region visualized in the left bottom panel, equivalent in scale to the Bolshoi simulation (Klypin, Trujillo-Gomez & Primack 2011). The evolution of the largest halo is visualized in Fig. 3.
Fig. 2 shows dark matter distribution of the Shin-Uchuu simulation at z = 0. The top panel shows a 140 |$\, h^{-1} \, \rm Mpc$| × 93 |$\, h^{-1} \, \rm Mpc$| slice of thickness of 17.5 |$\, h^{-1} \, \rm Mpc$|. The format is the same as in Fig. 1, where we again zoom-in on the largest structure in the box. Fig. 3 shows the evolution of three selected regions at redshifts z = 10.4, 5.2, 2.0, and 0.0: the largest cluster halo in the Uchuu simulation, a Milky Way-sized halo in the Shin-Uchuu simulation, and a void selected by eye in the Shin-Uchuu simulation. The evolution of the cosmic web leading to protocluster formation is clearly visible in the left row. In the centre row, thanks to the high resolution of the Shin-Uchuu simulation we observe many progenitor haloes of the Milky Way system, even at z > 10. More than 10 000 of Milky Way-sized haloes are formed in Shin-Uchuu, which enables us to study the statistics of such haloes with unprecedented resolution. In the right row, which tracks the evolution of a large cosmic void, we see how small haloes form even within such an underdense environment, highlighting both the large spatial volume and the high resolution of Shin-Uchuu.
Dark matter distribution of the higher resolution Shin-Uchuu simulation at z = 0. The top panel shows a 140 |$\, h^{-1} \, \rm Mpc$| × 93 |$\, h^{-1} \, \rm Mpc$| slice of thickness of 17.5 |$\, h^{-1} \, \rm Mpc$|. The three bottom panels zoom-in on the largest halo in Shin-Uchuu on scales of 35, 7.5, and 2.3 |$\, h^{-1} \, \rm Mpc$| (moving clockwise). The uppermost white box in the top panel is the same region visualized in the left bottom panel. The middle white box is a void region selected by eye, while the lowermost white box is a Milky Way-sized halo. The evolutionary paths of the latter two regions are visualized in Fig. 3.
Evolution of three different environments drawn from the Uchuu simulation suite. Redshift is marked in each panel, z = 10.4, 5.2, 2.0, and 0.0, from top to bottom. The three environments are: left, the largest halo in the Uchuu simulation; middle, a Milky Way-sized halo in the Shin-Uchuu simulation; and right, a void selected by eye in the Shin-Uchuu simulation. The side-lengths shown are 38, 2.3, and 35 |$\, h^{-1} \, \rm Mpc$| for the left-hand, middle, and right-hand panels, respectively.
3 RESULTS
We first present the basic properties of haloes, matter power spectra, and mass functions of the Uchuu simulations. Then, we propose an accurate model of halo concentrations that describes our simulations.
3.1 Power spectrum
Large number of particles and high force resolution of Uchuu simulations allow us to measure the power spectrum of dark matter fluctuations for a very large range of wavenumbers. However, in order to use this potential advantage, we need to implement a technique that is different from traditionally used method based on a large single mesh. We start with a single mesh of size Ng = 2400 in one dimension. The mesh covers the whole computational box L. The Cloud-In-Cell technique is applied to all particles Np to find the dark matter density on this mesh. In this process, the ‘weight’ of each particle is assumed to be |$W_1= N_{\rm g}^3/N_{\rm p}$|. In this case, the total ‘weight’ of all particles is simply the total number of grid points. Using the Fast Fourier Transform (FFT), we find the power spectrum of the density field. Because the mesh is not very large, it lacks information on wavenumbers larger than the Nyquist frequency kNy = (π/L)Ng of the mesh.
On the next step we again use the |$N_{\rm g}^3$| mesh, but this time it covers only half of the computational box, and, thus, it has box size L/2, and its Nyquist frequency is twice larger. When estimating the density, the coordinates of each particle are folded with the new box size: |$\tilde{x} = \mod (x,L/2)$| and the same is applied for y- and z-coordinates. The density assignment is made using the new coordinates |$(\tilde{x},\tilde{y},\tilde{z})$| and the particle weight is increased by factor 23/2. Again, we use the FFT to find the power spectrum. This time it does not have any information about waves longer than L/2 but it has information on frequencies that are twice higher than on the first step. We proceed with new levels each time reducing twice the box size, increasing twice the mesh Nyquist frequency, and increasing particle ‘weight’ by 23/2. In total, we have six levels of meshes with the combined range of wavenumbers from (2π/L) to 25Ng(2π/L).
The final power spectrum of the whole simulation is constructed from the set of six power spectra obtained for each mesh. We start with the first power spectrum corresponding to the box L. The power spectrum is corrected for the aliasing. All estimates are taken until we reach the points where the aliasing correction falls below 0.85. At this moment, we proceed to the results of the next mesh with twice the smaller box size. The process continues for all six levels of meshes.
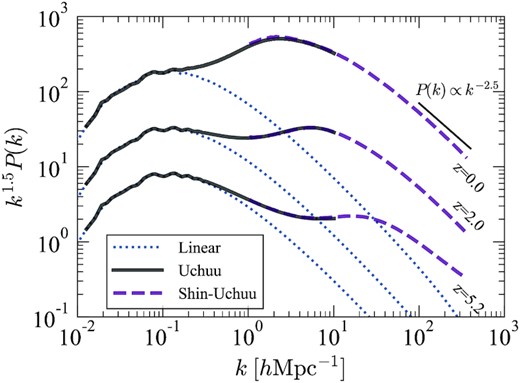
Fig. 4 shows the evolution of the power spectra of dark matter from the Uchuu and Shin-Uchuu simulations. The Uchuu suite allows us to plot a large range of wavenumbers covering five orders of magnitude. At low-k, the simulation follows the linear matter power spectrum. Power spectra are multiplied by k1.5, where k is the wavenumber, which clearly highlights the baryon acoustic oscillation (BAO) features, including the first and second peaks at k ∼ 0.07 and 0.13 |$\, h \, \, \rm Mpc^{-1}$| for z < 2. Other small peaks can be seen at z > 2, but these are gradually smeared out at lower redshift as the spectra is influenced by non-linear structure growth. Both simulations agree well with each other in the overlapping region, 1 < k < 10 |$\, h \, \, \rm Mpc^{-1}$|. The agreement is similar to that found by Schneider et al. (2016), who compared power spectra calculated by three different N-body methods and showed convergence at the 1 per cent level for k < 1 |$\, h \, \, \rm Mpc^{-1}$|, and 3 per cent level for k < 10 |$\, h \, \, \rm Mpc^{-1}$| when using standard run parameters. In their tests, gadget-3 (Springel 2005) was adopted, and its time-stepping method and choice of run parameters are similar to what was used in the Uchuu and the Shin-Uchuu simulations.
Power spectra of the Uchuu (solid curves) and Shin-Uchuu (dashed curves) simulations. Results are shown for z = 0.0, 2.0, and 5.2 (top to bottom), where each are multiplied by k1.5 to more clearly highlight the BAO features. The dotted curves show the linear power spectra. At high-k, the power is close to P(k) ∝ k−2.5.
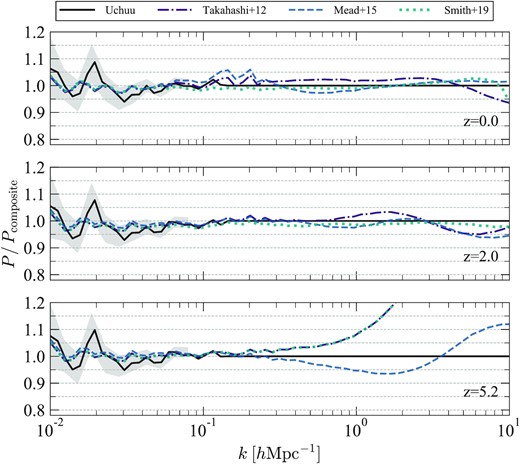
Fig. 5 shows a comparison between the Uchuu matter power spectra at low to middle-k with predictions from three models of non-linear structure evolution (Takahashi et al. 2012; Mead et al. 2015; Smith & Angulo 2019). The spectra of Mead et al. (2015) are calculated using hmcode,11 and of Takahashi et al. (2012) and Smith & Angulo (2019) using ngenhalofit.12 We construct the reference spectra Pcomposite as a composite of the Uchuu power spectrum for k > 0.1 |$\, h \, \, \rm Mpc^{-1}$|, and an average of an ensemble of 17 glam particle-mesh simulations (Klypin & Prada 2018) for k < 0.1 |$\, h \, \, \rm Mpc^{-1}$| to ameliorate the effects of cosmic variance. The glam simulations were run in 2 h−1 Gpc side-length boxes with 20003 particles moving in a 70003 mesh, providing 8.6 × 1010|$\, h^{-1}\, \rm M_{\odot }$| mass per particle resolution.
Comparison of power spectra at low-k with predictions from three models of the non-linear matter power spectrum (Takahashi et al. 2012; Mead et al. 2015; Smith & Angulo 2019). The top, middle, and bottom panels show the results for z = 0.0, 2.0, and 5.2, respectively. The reference spectra, Pcomposite, are taken from the Uchuu simulation for k > 0.1 |$\, h \, \, \rm Mpc^{-1}$| and an ensemble of glam simulations (Klypin & Prada 2018) for k < 0.1 |$\, h \, \, \rm Mpc^{-1}$|. The grey shaded regions are the estimated 1σ scatter of the Uchuu simulation.
The shaded regions in Fig. 5 show the estimated 1σ scatter of the Uchuu simulation, which overlaps with the composite power spectra, meaning that deviations of the simulation spectra at k < 0.1 |$\, h \, \, \rm Mpc^{-1}$| are due to the cosmic variance. For k > 0.1 |$\, h \, \, \rm Mpc^{-1}$|, the model prediction of Smith & Angulo (2019) agrees remarkably well with the Uchuu simulation at z = 0 and z = 2, where the error is within ∼2 per cent up to k = 10 |$\, h \, \, \rm Mpc^{-1}$|. As expected, this model fails to predict the spectra at z = 5.2 because it is not calibrated beyond z = 3 and reverts to that provided by Takahashi et al. (2012). The models of Takahashi et al. (2012) and Mead et al. (2015) predict the power within ∼5 per cent at z = 0.0 and 2.0. At z = 5.2, Mead et al. (2015) predict the power within ∼5 per cent at k < 4 |$\, h \, \, \rm Mpc^{-1}$|, which is better than the others, even though it is not calibrated for such high redshifts. In general, the accuracy at high redshift reflects how the underlying models are constructed.
These results demonstrate that our simulations are accurate across a wide dynamic range, from BAO to very small scales, reinforcing their usefulness for a wide range of applications.
3.2 Halo mass function
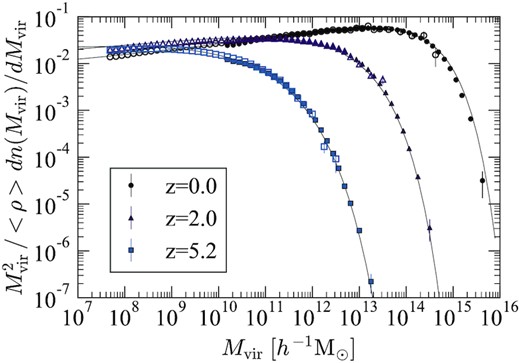
Fig. 6 shows the halo mass function multiplied by |$M_{\rm vir}^2$| and divided by the mean cosmic density for the Uchuu and the Shin-Uchuu simulations at z = 0, 2.0, and 5.2, where Mvir is the halo virial mass. We only consider haloes with more than 40 particles, corresponding to a minimum mass of 1.3 × 1010|$\, h^{-1}\, \rm M_{\odot }$| for Uchuu and 3.6 × 107|$\, h^{-1}\, \rm M_{\odot }$| for Shin-Uchuu. With this lower limit, the combined mass range spans approximately eight orders of magnitude, reflecting the power of our very large simulation set. The convergence between both simulations is remarkably good, within a few per cent.
Mass function of distinct haloes multiplied by |$M_{\rm vir}^2$| and divided by the mean cosmic density from the Uchuu (filled symbols) and the Shin-Uchuu (open symbols) simulations at z = 0.0, 2.0, and 5.2. These cover approximately eight orders of magnitude in halo mass. The error bars correspond to Poisson error. We only consider haloes with more than 40 particles. Solid curves show the fitting functions proposed by Despali et al. (2016).
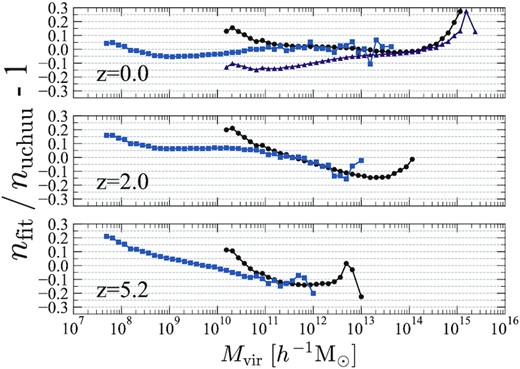
Fig. 6 also considers the halo mass fitting function proposed by Despali et al. (2016), shown by each solid line. The fractional difference between this function and each simulation is presented in Fig. 7 for Uchuu (filled circles) and Shin-Uchuu (filled squares). This comparison highlights a 5 per cent difference at z = 0 over a broad range of halo mass up to Mvir < ∼3 × 1014|$\, h^{-1}\, \rm M_{\odot }$|. Despali et al. (2016) present different parametrizations of their fitting function specifically for haloes more massive than Mvir > 3 × 1013|$\, h^{-1}\, \rm M_{\odot }$| (shown in their table 3). These provide a better fit in our analysis for Uchuu haloes of mass Mvir > 2 × 1014|$\, h^{-1}\, \rm M_{\odot }$|. Overall, we find a difference of less than 10 per cent for haloes with Mvir < 1015|$\, h^{-1}\, \rm M_{\odot }$|. At z = 2.0 and 5.2, this difference increases to around 10 per cent. At the massive end of the mass function, the fitting function underestimates the number of massive haloes, while it overestimates the number of less massive haloes. We expect this is related to challenges of cosmic variance and the accuracy of the simulations used to derive the fitting function (see also Knebe et al. 2013).
We do not perform an extensive analysis of the mass function in this paper but leave it for a dedicated study at a later time.
3.3 Subhalo mass function
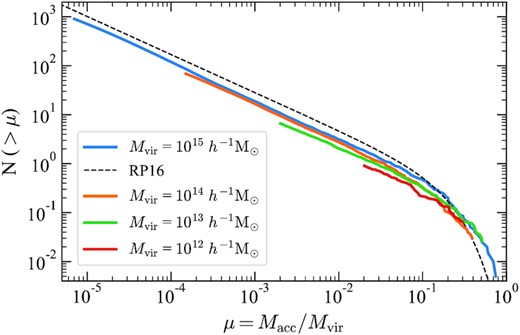
In Fig. 8, we display the mean subhalo mass function for the Uchuu simulation at z = 0, N(> Macc/Mvir) computed in four narrow (5 per cent) bins of host halo mass, Mvir = 1015, 1014, 1013, and 1012|$\, h^{-1}\, \rm M_{\odot }$|, where the subhalo mass Macc is defined at the time of first accretion. Solid lines with different colours correspond to different host halo mass bins as labelled in the figure panel. Overall our results are in good agreement with previous simulation works and model predictions (e.g. Rodríguez-Puebla et al. 2016; Hiroshima, Ando & Ishiyama 2018; van den Bosch & Ogiya 2018; van den Bosch et al. 2018, and references therein) that explore the subhalo mass function shape and host halo mass dependence. This figure also shows the best-fitting Schechter-like function (dotted line) to the Bolshoi Planck/MultiDark Planck subhalo mass function of host halo mass Mvir = 1015|$\, h^{-1}\, \rm M_{\odot }$| (see Rodríguez-Puebla et al. 2016). We highlight the remarkable agreement of the slope at the low-mass end, equal to −0.75, in agreement with previously reported works. Yet, the results obtained from Uchuu reveal a clear difference in the shape at the exponential tail, thanks to our superb statistics, with a shallow decline towards higher Macc/Mvir values. The ∼20 per cent difference in normalization is due to the difference in the adopted cosmological parameters among both simulation suites. A detailed study and interpretation of these results will be presented in a forthcoming paper (Moliné et al., in preparation).
The Uchuu subhalo mass function at z = 0, N(> μ), for different host haloes as a function of μ = Macc/Mvir (solid curves). As a reference, the dashed line shows the best-fitting Schechter-like function fit to the Bolshoi Planck/MultiDark Planck simulations (Rodríguez-Puebla et al. 2016). Note the similar overall power-law slope but different shape at the exponential tail due to the much higher statistics of Uchuu.
3.4 Mass–concentration relation: all haloes
The mass–concentration relation is an essential diagnostic to characterize the internal structure of haloes. Many past studies have investigated the dependence of concentration on halo mass and redshift (e.g. Ludlow et al. 2012; Prada et al. 2012; Dutton & Macciò 2014; Correa et al. 2015; Klypin et al. 2016; Okoli & Afshordi 2016; Pilipenko et al. 2017; Child et al. 2018; Diemer & Joyce 2019; Ishiyama & Ando 2020). These works show that halo concentration increases with decreasing halo mass and redshift, with the exception of the most massive and rare haloes for which the concentration may increase with increasing mass (e.g. Prada et al. 2012; Klypin et al. 2016; Diemer & Joyce 2019). Halo concentration also depends on the background cosmology and the relaxation state of haloes (e.g. Dutton & Macciò 2014; Klypin et al. 2016), with relaxed haloes exhibiting slightly larger concentrations.
In this paper, we extend these past works thanks to the statistical power of the Uchuu simulation suite, which covers an unprecedented range in halo mass at high resolution. For haloes with an NFW profile (Navarro, Frenk & White 1997), concentration is defined as the ratio of the halo radius to the characteristic radius rs of the NFW profile. In general, there are different ways to define the halo radius and mass. Here we use two methods, with haloes defined either by the radius r200 where the average spherical overdensity is 200 times the critical density, or by the virial overdensity that slightly evolves with the redshift. We will label quantities related to each of the definitions by the indexes ‘200’ or ‘vir’, respectively. Unless otherwise noted, our main results are shown with r200. An alternative definition, using r500, is often used for galaxy cluster modelling, in which the average spherical overdensity is 500 times the critical density.
For haloes well fit by an NFW profile, two parameters – mass and concentration – uniquely define the density distribution. The situation is more complicated for haloes that do not follow an NFW profile. Indeed, some haloes (and especially very massive and rare ones) are better described by the Einasto profile (Navarro et al. 2004; Dutton & Macciò 2014; Klypin et al. 2016). In this case, one needs three parameters. If we still choose to use only two – mass and concentration – how do we then define the concentration? One must be careful when taking the naive association of the core radius as the radius r−2 where the log–log slope of the density profile is −2, which is valid for the NFW profile. In this case, two haloes with obviously different concentrations may have the same r−2 because they have different shape parameters of the Einasto profile. Indeed, Klypin et al. (2016) present examples that this typically happens with massive haloes. We similarly show cases of halo profiles of this kind in Appendix A. Keeping the above caveats in mind, for consistency in our analysis we use the same definition of concentration and the same algorithm as in the case of the two-parameter NFW profile. For such haloes, the accuracy of the prediction of their density distribution is reduced. However, in practice the errors for such haloes are relatively small, even in extreme cases. For example, the density profile errors are less than 5 per cent for the most massive haloes at z = 0 at radii larger than 0.01 of the halo radius.
Halo concentration also depends on the dynamical state of the halo, with relaxed haloes tending to have larger concentrations (e.g. Ludlow et al. 2012; Prada et al. 2012; Klypin et al. 2016). The selection criteria for relaxed haloes can differ in literature, and can introduce systematic biases. For example, Prada et al. (2012) found an upturn in the concentrations of massive haloes in both their ‘all’ and ‘relaxed’ samples, while Ludlow et al. (2012) did not find such an upturn in their relaxed ones. In this section, we use all haloes regardless of their relaxation state. Relaxed haloes and the upturn are discussed in the next section.
Appendix A presents estimates of the errors for different methods and the dependences of the estimates on numerical effects such as the number of particles and force resolution. There is a general trend that follows from the nature of the methods. The Vmax is sensitive to the mass distribution in the relatively peripheral region of a halo and it is not sensitive to the mass distribution at the centre or to any local fluctuations. This is a good method, if one is interested in the main body of the halo, but not its centre. The density fitting method is more sensitive to the central regions. However, it is also prone to errors produced by non-relaxed features.
Both definitions produce similar values at lower redshifts, z < 1, where haloes tend to be more relaxed. On average, the differences in concentration are less than few per cent. However, when the fraction of non-relaxed haloes increase (either at high redshifts or at the high-mass end) cfit results in smaller concentrations (Dutton & Macciò 2014). At z = 5, the difference between the two estimates can reach up to 15 per cent. See Appendix A for more details.
Best-fitting parameters of the mass–concentration relation for the model equation (2). Parameters are given for different methods of finding concentrations, for different halo selections, and for different halo definitions. We present concentration c500 estimated using only the profile fitting because it is better to describe the halo inner profile than the Vmax method as shown in Appendix A.
| c . | κ . | a0 . | a1 . | b0 . | b1 . | cα . |
|---|---|---|---|---|---|---|
| Vmax all haloes | ||||||
| c200 | 1.10 | 2.30 | 1.64 | 1.72 | 3.60 | 0.32 |
| cvir | 0.76 | 2.34 | 1.82 | 1.83 | 3.52 | −0.18 |
| Fit all haloes | ||||||
| c200 | 1.19 | 2.54 | 1.33 | 4.04 | 1.21 | 0.22 |
| cvir | 1.64 | 2.67 | 1.23 | 3.92 | 1.30 | −0.19 |
| c500 | 1.83 | 1.95 | 1.17 | 3.57 | 0.91 | 0.26 |
| Vmax relaxed haloes | ||||||
| c200 | 1.79 | 2.15 | 2.06 | 0.88 | 9.24 | 0.51 |
| cvir | 2.40 | 2.27 | 1.80 | 0.56 | 13.24 | 0.079 |
| Fit relaxed haloes | ||||||
| c200 | 0.60 | 2.14 | 2.63 | 1.69 | 6.36 | 0.37 |
| cvir | 1.22 | 2.52 | 1.87 | 2.13 | 4.19 | −0.017 |
| c500 | 0.38 | 1.44 | 3.41 | 2.86 | 2.99 | 0.42 |
| c . | κ . | a0 . | a1 . | b0 . | b1 . | cα . |
|---|---|---|---|---|---|---|
| Vmax all haloes | ||||||
| c200 | 1.10 | 2.30 | 1.64 | 1.72 | 3.60 | 0.32 |
| cvir | 0.76 | 2.34 | 1.82 | 1.83 | 3.52 | −0.18 |
| Fit all haloes | ||||||
| c200 | 1.19 | 2.54 | 1.33 | 4.04 | 1.21 | 0.22 |
| cvir | 1.64 | 2.67 | 1.23 | 3.92 | 1.30 | −0.19 |
| c500 | 1.83 | 1.95 | 1.17 | 3.57 | 0.91 | 0.26 |
| Vmax relaxed haloes | ||||||
| c200 | 1.79 | 2.15 | 2.06 | 0.88 | 9.24 | 0.51 |
| cvir | 2.40 | 2.27 | 1.80 | 0.56 | 13.24 | 0.079 |
| Fit relaxed haloes | ||||||
| c200 | 0.60 | 2.14 | 2.63 | 1.69 | 6.36 | 0.37 |
| cvir | 1.22 | 2.52 | 1.87 | 2.13 | 4.19 | −0.017 |
| c500 | 0.38 | 1.44 | 3.41 | 2.86 | 2.99 | 0.42 |
Best-fitting parameters of the mass–concentration relation for the model equation (2). Parameters are given for different methods of finding concentrations, for different halo selections, and for different halo definitions. We present concentration c500 estimated using only the profile fitting because it is better to describe the halo inner profile than the Vmax method as shown in Appendix A.
| c . | κ . | a0 . | a1 . | b0 . | b1 . | cα . |
|---|---|---|---|---|---|---|
| Vmax all haloes | ||||||
| c200 | 1.10 | 2.30 | 1.64 | 1.72 | 3.60 | 0.32 |
| cvir | 0.76 | 2.34 | 1.82 | 1.83 | 3.52 | −0.18 |
| Fit all haloes | ||||||
| c200 | 1.19 | 2.54 | 1.33 | 4.04 | 1.21 | 0.22 |
| cvir | 1.64 | 2.67 | 1.23 | 3.92 | 1.30 | −0.19 |
| c500 | 1.83 | 1.95 | 1.17 | 3.57 | 0.91 | 0.26 |
| Vmax relaxed haloes | ||||||
| c200 | 1.79 | 2.15 | 2.06 | 0.88 | 9.24 | 0.51 |
| cvir | 2.40 | 2.27 | 1.80 | 0.56 | 13.24 | 0.079 |
| Fit relaxed haloes | ||||||
| c200 | 0.60 | 2.14 | 2.63 | 1.69 | 6.36 | 0.37 |
| cvir | 1.22 | 2.52 | 1.87 | 2.13 | 4.19 | −0.017 |
| c500 | 0.38 | 1.44 | 3.41 | 2.86 | 2.99 | 0.42 |
| c . | κ . | a0 . | a1 . | b0 . | b1 . | cα . |
|---|---|---|---|---|---|---|
| Vmax all haloes | ||||||
| c200 | 1.10 | 2.30 | 1.64 | 1.72 | 3.60 | 0.32 |
| cvir | 0.76 | 2.34 | 1.82 | 1.83 | 3.52 | −0.18 |
| Fit all haloes | ||||||
| c200 | 1.19 | 2.54 | 1.33 | 4.04 | 1.21 | 0.22 |
| cvir | 1.64 | 2.67 | 1.23 | 3.92 | 1.30 | −0.19 |
| c500 | 1.83 | 1.95 | 1.17 | 3.57 | 0.91 | 0.26 |
| Vmax relaxed haloes | ||||||
| c200 | 1.79 | 2.15 | 2.06 | 0.88 | 9.24 | 0.51 |
| cvir | 2.40 | 2.27 | 1.80 | 0.56 | 13.24 | 0.079 |
| Fit relaxed haloes | ||||||
| c200 | 0.60 | 2.14 | 2.63 | 1.69 | 6.36 | 0.37 |
| cvir | 1.22 | 2.52 | 1.87 | 2.13 | 4.19 | −0.017 |
| c500 | 0.38 | 1.44 | 3.41 | 2.86 | 2.99 | 0.42 |
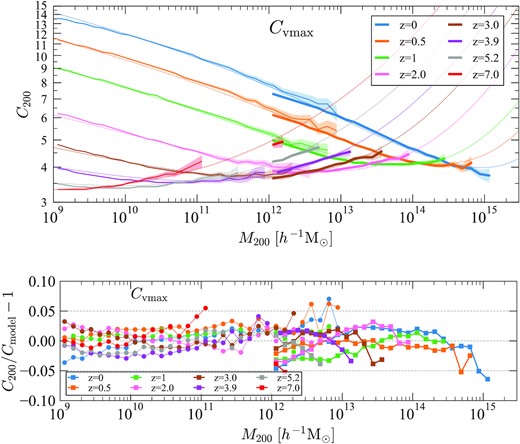
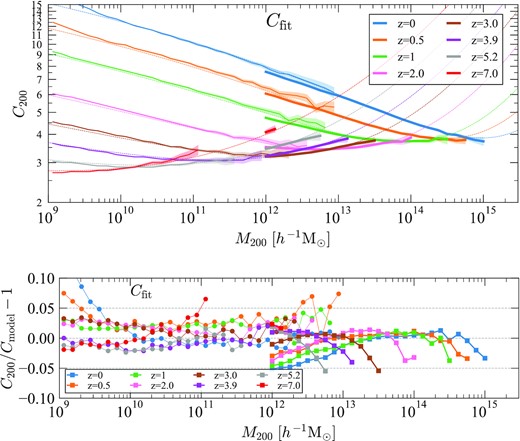
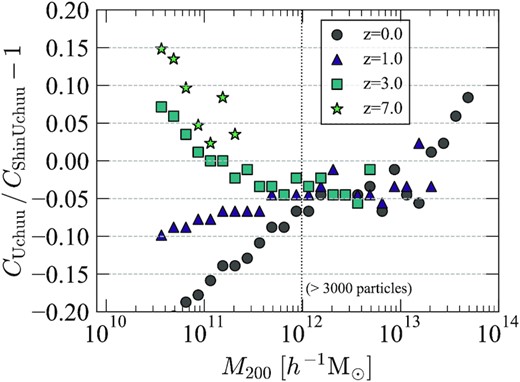
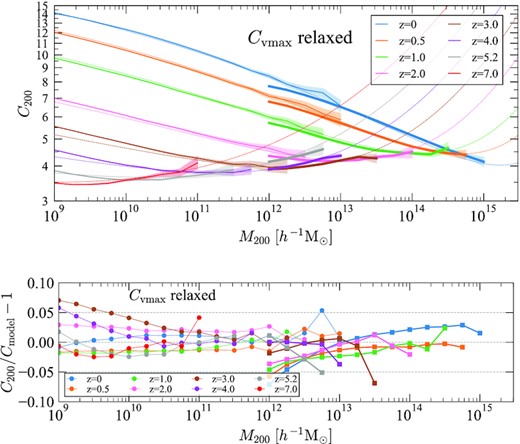
Fig. 9 (top panel) shows the mass–concentration relation of the Uchuu and Shin-Uchuu simulations and their redshift evolution. Median values with statistical uncertainty in each mass bin are shown. The concentrations are estimated using the Vmax method (equation 1). At low redshift, the relation follows a well-known power-law behaviour except at the highest masses. We observe a flattening and an upturn with increasing mass, consistent with previous findings (e.g. Prada et al. 2012). This flattening and upturn gradually shifts to lower mass at higher redshift. The Shin-Uchuu simulation produces slightly larger concentrations than Uchuu in the overlap region (1012–1013|$\, h^{-1}\, \rm M_{\odot }$|) at z < 3. However, both simulations follow the same trend. Fig. 10 (top panel) also shows the mass–concentration relation, but where concentrations are estimated by the profile fitting method. Together, Figs 9 and 10 highlight that the main tendencies of the concentration–mass relation does not depend on the method to find concentration in our simulation suite. This includes the upturn in the concentration at large masses.
Top panel: Mass–concentration relation of haloes for the Uchuu (thick curves) and the Shin-Uchuu (thin curves) simulations. Median values with statistical uncertainties in each mass bin are shown. The concentrations are estimated using Vmax given by equation (1). The dashed curves are predictions of the analytical model described by equation (2) in Appendix B. Bottom panel: The fractional difference between the halo concentrations of the Uchuu (squares) and the Shin-Uchuu (circles) simulations and the model predictions. It illustrates that the analytical model provides an accurate fit to the actual concentrations with an error less than ∼5 per cent, for the redshift range 0 < z < 7 and halo masses covering six orders of magnitude.
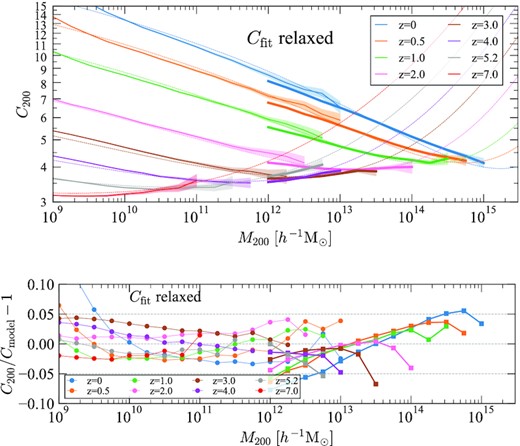
The same as in Fig. 9 but for concentrations estimated by profile fitting. The plot shows that the main tendencies of the concentration–mass relation do not depend on the method used to find the concentration. This includes the upturn in concentration found at large masses.
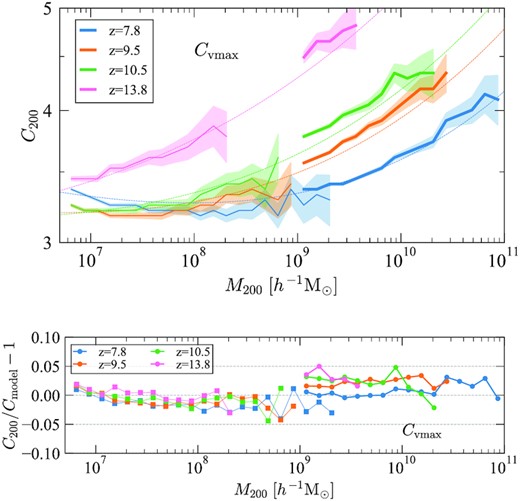
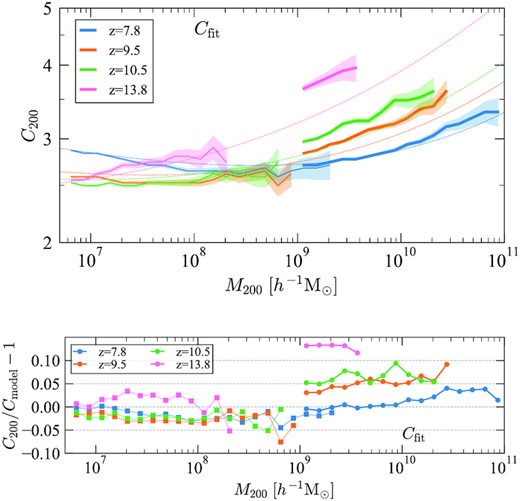
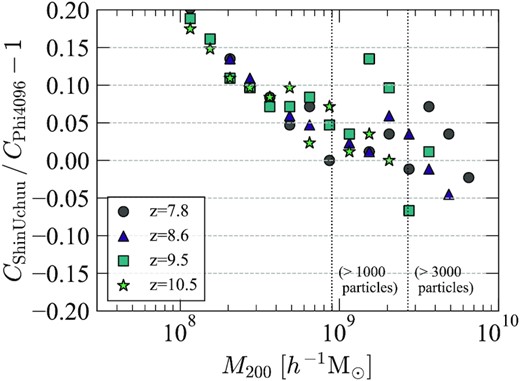
With the unprecedented high resolution and statistical power of the Shin-Uchuu and the Phi-4096 simulations, we can statistically study the mass–concentration relation at mass M200 < 1011|$\, h^{-1}\, \rm M_{\odot }$| and redshift z > 7 for the first time. The top panels of Figs 11 and 12 show the mass–concentration relation of the Shin-Uchuu and Phi-4096 simulations and their redshift evolution, using the Vmax and profile fitting methods, respectively. For both, concentration increases with increasing mass, opposite to the behaviour seen at lower redshift. This should be compared to the flattening and upturn identified in Figs 9 and 10. Again, the main trends of the concentration–mass relations do not depend on the method to find concentration.
Halo concentrations at very large redshifts and small masses. Top panel: Mass–concentration relation for the Shin-Uchuu (thick curves) and the Phi-4096 (thin curves) simulations. In both cases, concentrations are estimated using the Vmax method. Median values with statistical uncertainty in each mass bin are shown. The dashed curves provide the model prediction described by equation (2). Bottom panel: The fractional difference between the halo concentrations of the Shin-Uchuu (circles) and the Phi-4096 (squares) simulations and the analytical model. Again, we find the model fits the simulation with an accuracy of better than ∼5 per cent across a large redshift and mass range.
The same as in Fig. 11 but for concentrations estimated by profile fitting.
The bottom panel of both Figs 9 and 11 shows residuals of the concentration estimated using the Vmax method relative to the model. Across most of the halo mass and redshift range the difference is within 5 per cent, although there are a few exceptions. This highlights that the accuracy provided by the model is quite good for masses spanning nearly eight orders of magnitude. Similarly, the bottom panel of both Figs 10 and 12 show residuals using the profile fitting method. The model accuracy here is also good but slightly worse than for concentrations estimated using Vmax. Again, the difference is within 5 per cent for most halo masses and redshifts, although it can increase to nearly 10 per cent in places. This is prominent for rare objects at high redshift.
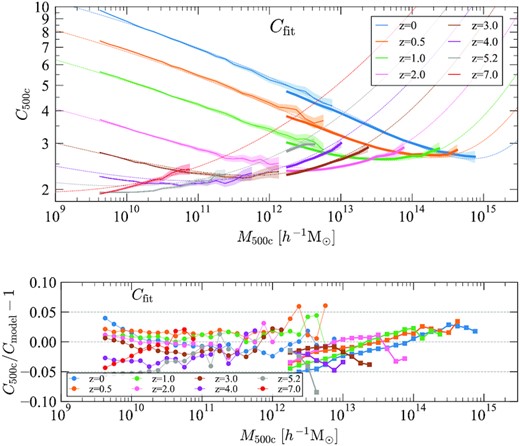
We also explore the concentration relation using r500: |$\rm c_{500} = r_{500}/r_s$|. The same fitting procedure described in this section is used to find the best-fitting parameters of the mass–concentration relation. Plots for concentration–mass relation are presented in Fig. C1. We present concentration estimated using only the profile fitting because it is better to describe the halo inner profile than the Vmax method as shown in Appendix A. We use only data at z ≤ 7 to ensure the fitting error within 5 per cent. Including data at z > 7, the fitting error increases from 5 to 10 per cent.
Table 2 presents the parameters for the c200, cvir, and c500 halo definitions estimated using the Vmax and profile fitting methods. In general, the model accuracy is very similar for c200; the difference is within 5 per cent for most halo masses and redshifts but is close to 10 per cent for rare objects at high redshift when concentrations are estimated by profile fitting.
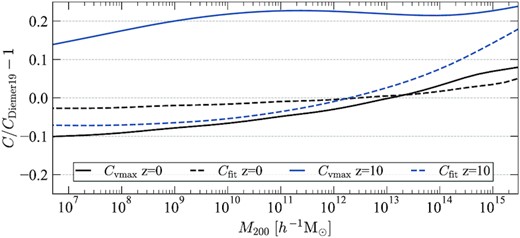
In spite of the fact that we use the same functional form proposed by Diemer & Joyce (2019), our parameters of the approximation are quite different from theirs. Fig. 13 compares predictions for such concentrations. The agreement between the predictions is remarkably good for cfit estimates at z = 0 with just ∼2 per cent differences for masses M < 5 × 1014|$\, h^{-1}\, \rm M_{\odot }$|. The differences increase at high redshifts and become ∼20 per cent at z = 10. This is a good improvement as compared with the situation just a few years ago. For example, disagreement between Correa et al. (2015) and Diemer & Kravtsov (2015) was 20 per cent at z = 0, M = 2 × 1014|$\, h^{-1}\, \rm M_{\odot }$|. A more detailed comparison of results provided by different publications can be found in Diemer & Joyce (2019).
Comparison of the predictions of halo concentrations c200 in this paper with those of Diemer & Joyce (2019). Both predictions use the same functional form but different parameters.
3.5 Mass–concentration relation: relaxed haloes
So far we have presented mass–concentration relations for all haloes regardless of their dynamical state. For some studies, one may need to remove rare transient events (e.g. due to ongoing major mergers) and to study more relaxed haloes (e.g. Neto et al. 2007; Ludlow et al. 2012; Prada et al. 2012; Klypin et al. 2016). There are no clear selection criteria of relaxed haloes.
The first obvious choice is the virial parameter 2K/|W| − 1, where W and K are the potential and kinetic energies, respectively. The virial parameter should be equal to zero for objects in virial equilibrium. As such, this parameter has been extensively used in the past (e.g. Neto et al. 2007; Ludlow et al. 2012). However, many results show that otherwise relaxed haloes can have systematically too large a 2K/|W| − 1, as if the kinetic energy is too big for a given potential energy. The problem is extreme with values 2K/|W| − 1 > 0.3 being typical for haloes at redshifts z > 3 (Davis, D’Aloisio & Natarajan 2011; Klypin et al. 2016). If this were true, haloes would have dissolved or collapsed on a dynamical time-scale. Analysis of individual and average halo profiles does not show any signs of catastrophic collapse or expansion: inner halo regions have zero average radial velocities while there are small infalling velocities close to the virial radius. This failure of the virial parameter is attributed to simplistic treatment of the virial theorem. Dark matter haloes are not isolated objects. When applying the virial theorem, one must include the surface pressure term, which, for spherical haloes, is |$S_{\rm p}=4\pi R^3_{\rm vir}\rho _{\rm vir}v_{\rm r}^2$|, where |$v_{\rm r}^2$| is the dispersion of the radial velocity. Once this correction is applied, the virial parameter becomes significantly smaller (Shaw et al. 2006; Davis et al. 2011; Klypin et al. 2016). Furthermore, large and complicated corrections and uncertainties due to non-spherical halo shapes make the virial parameter much less useful as an indicator of non-equilibrium haloes. This is why the virial parameter is currently either not utilized or used with a very large upper limit (Correa et al. 2015; Klypin et al. 2016; Child et al. 2018).
There are other conditions for selecting relaxed haloes. These include the fraction of mass in subhaloes fsub, the offset parameter Xoff, and the spin parameter λ. We define the offset parameter as the distance between the centre of haloes and centre of mass: |$X_{\rm off}=|\vec {r}_{\rm center}-\vec {r}_{\rm cm}|/R_{\rm vir}$|. The spin parameter is defined as |$\lambda = J|E|^{1/2}/GM^{5/2}_{\rm vir}$|, where E is the total energy and J is the angular momentum.
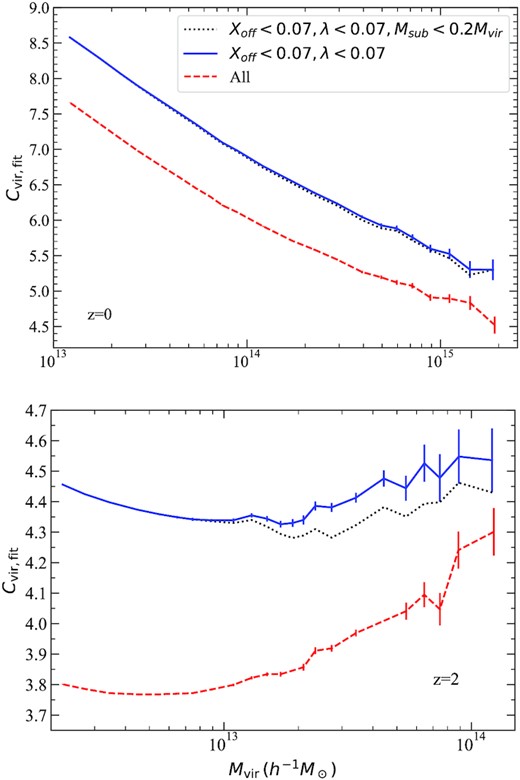
Fig. 14 compares concentrations of relaxed and all haloes at z = 0 and z = 2 (solid curves). Here, we focus on the high-mass part of the concentration–mass relation. Appendix C presents further plots of the concentration of relaxed haloes. We also use another set of conditions to select relaxed haloes: in addition to the main conditions in equation (3) we also remove haloes if the mass of the largest subhalo exceeds 20 per cent of halo mass (dotted curves).
Comparison of concentrations of massive relaxed and all haloes at z = 0 (top panel) and z = 2 (bottom panel). Here, we use virial masses and concentrations. The full curves show concentrations of haloes restricted by the offset parameter Xoff < 0.07 and spin parameter λ < 0.07. The dotted curves are for haloes with an extra condition: we remove haloes with the most massive subhalo exceeding 20 per cent of the mass of the central halo. The error bars show the statistical uncertainties of the average values of the concentrations. Note the dramatic difference between z = 0 and z = 2 concentrations: no upturn at z = 0 and a prominent upturn at z = 2. The upturn is weaker but still present for relaxed haloes regardless of which of the two sets of conditions are used. For all redshifts and halo masses, halo concentration is larger for relaxed haloes compared with the full population.
The most notable feature in this figure is the dramatic difference between z = 0 and z = 2 concentrations. At z = 0, there is no indication of an upturn in the concentration–mass relation, though the relation is not a power law as is the case for much smaller haloes. At z = 2, there is a prominent upturn in the population of all haloes. The upturn is weaker but still present for relaxed haloes regardless of which of the two sets of conditions are used.
For all redshifts and for all halo masses, halo concentration is larger for relaxed haloes. The additional constraint on the mass of the largest subhalo fsub < 0.2 does not affect much the concentration–mass relation. It is barely noticeable at z = 0. At z = 2, the effect is larger but still small. There is a good reason for this: conditions for the offset Xoff < 0.07 and spin λ < 0.07 have already removed most of the major-merger events. This can be clearly seen from the fraction of relaxed haloes. For example, at z = 2 the fraction of relaxed haloes with masses Mvir > 8 × 1013|$\, h^{-1}\, \rm M_{\odot }$| is 43 per cent of the total 900 haloes. Adding the constraint on subhaloes only removes another 5 per cent of haloes. We also tried to mimic one of the selection conditions used by Ludlow et al. (2012) by removing haloes having their total mass of subhaloes larger than 10 per cent of the halo mass. This reduces the fraction of relaxed haloes to 30 per cent without much of an effect on the upturn (we find only an additional 1.7 per cent decline of halo concentration at the upturn).
One of the contentious issues in this field is the existence and nature of an upturn in the halo concentration–halo mass relation at the massive end. It was first discovered by Klypin et al. (2011) and later confirmed by Prada et al. (2012), Dutton & Macciò (2014), Diemer & Kravtsov (2015), Klypin et al. (2016), and Diemer & Joyce (2019). There is a general consensus that the phenomenon is real as far as the population of all haloes is concerned. However, there are widely different opinions regarding its nature.
Analytical models for the evolution of halo concentrations so far do not help us understand the nature of the upturn. Those used by Prada et al. (2012), Diemer & Kravtsov (2015), and Diemer & Joyce (2019) assume the upturn, so it is not an argument in favour of it. Models that relate the evolution of the halo concentration with the mass accretion history (Bullock et al. 2001; Zhao et al. 2009; Correa et al. 2015) assume that the concentration increases as the halo accretes mass after an episode of major merger. Again, these models do not predict the upturn. The problem is that mass accretion history is not the only factor that defines halo concentration. Simulations of Klypin et al. (2016) clearly show that haloes at the upturn have much more radial orbits when compared with haloes at the declining branch of the concentration–mass relation (see e.g. fig. 14 in Klypin et al. 2016). In turn, large radial velocities of dark matter particles result in more mass reaching small radii, which is the reason for increased concentration. We find the same effect in the Uchuu simulation.
Finding the upturn in cosmological simulations is a difficult numerical problem because it requires relatively high mass resolution and a very large simulation box to have enough statistics of massive haloes. For example, Correa et al. (2015) did not find the upturn in either the total population or in relaxed haloes. However, their largest computational box was only 400|$\, h^{-1} \, \rm Mpc$|. The only chance for them to see the upturn was at z = 2: at lower redshifts the upturn is weaker and at higher redshifts their computational box and mass resolution are too small to resolve the required population. The largest haloes at z = 2 in Correa et al. (2015) had mass ∼1013|$\, h^{-1}\, \rm M_{\odot }$|, and statistical uncertainties for the concentration of these haloes were ∼10 per cent. They did not see the upturn because it starts at masses larger than M = 1013|$\, h^{-1}\, \rm M_{\odot }$| (see Figs 9 and 14).
A similar situation happens for simulations of Dutton & Macciò (2014) who had larger box of 1 |$\, h^{-1} \, \rm Gpc$| (with thus improved statistics) but a mass resolution of 4 × 1011|$\, h^{-1}\, \rm M_{\odot }$|. Thus, again we do not expect them to see the upturn because their largest halo of M = 2 × 1013|$\, h^{-1}\, \rm M_{\odot }$| had only 50 particles – not enough to estimate the concentration. Other boxes with better mass resolution were too small to definitively find the upturn.
Our results for relaxed haloes contradict those of Ludlow et al. (2012) who argue that once unrelaxed haloes are removed, the concentration of the remaining massive haloes declines, resulting in the disappearance of the upturn (see their fig. 1). When we remove unrelaxed haloes in Uchuu simulation, the concentration increases for all haloes including those in the upturn. It is interesting to explore why we have such disagreements. Ludlow et al. (2012) used three conditions to select ‘relaxed haloes’: 2K/|W| < 1.3, Xoff < 0.07 and the fraction of mass in subhaloes fsub < 0.1. At first sight, these conditions are similar to what we use in Fig. 14. As discussed above, as a test we also implemented the condition fsub < 0.1 but it did not make much of a difference. In spite of the seemingly similar conditions, the overall disagreement with Ludlow et al. (2012) is quite dramatic. This can be illustrated by comparing the fractions of relaxed haloes at z = 2–3. In Uchuu simulation, this fraction is about 30 per cent once we add a constraint on the mass of subhaloes. In the case of Ludlow et al. (2012), their fraction of relaxed haloes were significantly smaller: 2 per cent at z = 3 and 11 per cent at z = 1. The reason for the small fraction of relaxed haloes is due to smaller cutoff of the virial parameter used by Ludlow et al. (2012). As discussed in Section 3.5, without a correction for the surface pressure the virial parameter provides very biased results, giving the impression that most of the high-redshift massive haloes are out of virial equilibrium, while in reality they are not. Figs 5 and 6 in Klypin et al. (2016) show the effect of this surface pressure correction, which has a strong dependence on redshift. At z = 3, the vast majority of haloes would violate the condition 2K/|W| < 1.3 used by Ludlow et al. (2012), and thus are considered unrelaxed. After the correction, most of them pass this condition and become ‘relaxed enough’ again. Thus, we can conclude that the disagreement with Ludlow et al. (2012) is due to an unrealistic constraint on the virial parameter used in their analysis.
We can also now settle another issue: is there an upturn at z = 0? The argument for the presence of late-redshift upturn was always statistically questionable. With the large volume of the Uchuu simulation, we can clearly state that there is no z = 0 upturn.
4 SUMMARY AND FUTURE PROSPECTS
Ongoing and upcoming wide and deep surveys will provide vast amounts of data on galaxies and AGNs over Gpc scales. To get as much information as possible from such surveys, precise mock galaxy and AGN catalogues are needed. For this purpose, we conducted a suite of ultralarge cosmological N-body simulations, the Uchuu simulation suite, and constructed halo/subhalo merger trees for them. The largest simulation in the suite, Uchuu, consists of 12 8003 dark matter particles in a box of 2.0 |$\, h^{-1} \, \rm Gpc$|, with particle mass of 3.27 × 108|$\, h^{-1}\, \rm M_{\odot }$|. The highest resolution simulation in the suite, Shin-Uchuu, consists of 64003 particles in a 140 |$\, h^{-1} \, \rm Mpc$| box, with particle mass of 8.97 × 105|$\, h^{-1}\, \rm M_{\odot }$|. By combining these simulations, we can follow the evolution of dark matter haloes (and subhaloes) spanning the mass range from dwarf galaxies to massive galaxy clusters. Thanks to its large volume and high-mass resolution, our simulation suite provides one of the most accurate theoretical templates to date to construct galaxy and AGN catalogues.
In this paper, we have presented the basic properties of the Uchuu suite, which includes halo demographics, the matter power spectra, and halo and subhalo mass functions. These demonstrate the very large dynamical range and superb statistics of the Uchuu simulations. Then, we provided an accurate model of halo concentrations that describes our simulations. The results are summarized as follows.
From the analysis of the evolution of power spectra, we have demonstrated that our simulations are accurate for use across a wide dynamic range, from the BAO scale down to very small structures.
We have shown the halo mass function with a mass range spanning approximately eight orders of magnitude, reflecting the power of our very large simulation set. The convergence between simulations is remarkably good – within a few per cent – ensuring the accuracy of our results.
The subhalo mass function, with Macc/Mvir ranging about six orders of magnitude, is in good agreement with previous simulation work and various model predictions. Yet, our superb statistics reveal a clear difference at the high-mass exponential tail, with a shallow decline towards higher Macc/Mvir values.
Using the Uchuu suite, we have calibrated the parameters of the halo concentration evolution model presented in Diemer & Joyce (2019). Our fitting errors are within 5 per cent for haloes with masses spanning nearly eight orders of magnitude and covering the redshift range 0 ≤ z ≤ 14.
We confirm that there is an upturn in the mass–concentration relation for the population of all haloes and of relaxed haloes at redshifts z ≳ 0.5. There is no upturn at lower redshifts.
The data products used in this paper form part of the Uchuu public DR1, and can be found at http://skiesanduniverses.org/. This includes subsets of simulation particles, matter power spectra, halo/subhalo catalogues, and their merger trees. The latter will be described in an upcoming publication, and are produced by post-processing the data with the well-established tools rockstar (Behroozi et al. 2013a) and consistent trees (Behroozi et al. 2013b). Particle data are provided in the gadget-ii format (Springel 2005); selected other products use the hdf5 format to help reduce reading and analysis times. This public data release increases the accessibility and portability of our data and provides new opportunities for scientific exploitation.
The superb numerical resolution achieved by the Uchuu simulations over an extremely wide halo mass range makes them uniquely powerful to characterize the subhalo population in great detail as well. Indeed, in a forthcoming publication (Moliné et al., in preparation) the full set of Uchuu simulations in Table 1, together with the Phi-4096 high-resolution simulation described in Table 1, will be used to study subhalo concentrations, abundances, and distributions. Potential dependences of subhalo properties with, e.g. host halo mass or distance to host halo centre will also be explored. All together, we anticipate that Uchuu and Phi-4096 will allow us to test, under the same consistent framework, subhalo maximum circular velocities as low as |$\rm \sim 1~km\,s^{-1}$| and as high as |$\rm \sim 1800~km\,s^{-1}$| or, equivalently, subhalo masses between ∼105 and 1015 h−1 M⊙, with unprecedented statistics. This impressive subhalo mass range will thus enable the study of halo hierarchy over several orders of magnitude, indeed reaching subhaloes as light as 10−7 the mass of their hosts for some haloes. In addition to its inherent cosmological value, this upcoming work on Uchuu halo substructure will be of particular interest to a large variety of topics currently under debate and scrutiny in adjacent fields. For instance, it may serve to elucidate the precise role of subhaloes for dark matter searches, e.g. Ackermann et al. (2012), Sánchez-Conde & Prada (2014), Moliné et al. (2017), Coronado-Blázquez et al. (2019), Ishiyama & Ando (2020); or to shed further light on the actual survival of subhaloes within their hosts (van den Bosch & Ogiya 2018; van den Bosch et al. 2018; Meneghetti et al. 2020).
The Uchuu suite of simulations will be used to produce a number of gravitational lensing studies and publicly available products. Light-cones of three different sizes (640, 340, and 123 deg2) and depths have been constructed from the simulation snapshots and projected on to a series of shells. Ray tracing through these cones using a modified version of the glamer (Metcalf & Petkova 2014; Petkova, Metcalf & Giocoli 2014) code has been done to produce maps of shear, convergence, and deflection for a range of source redshifts from 0 to 7 with one arcsecond resolution. For DR1, these maps are being made public along with accurate shear power spectra, correlation functions, and the halo–shear correlations. In addition, source catalogues with random positions and known redshift distributions will be provided so that users can sample from them for Monte Carlo calculations. In further data releases, with semi-analytical and halo occupation distribution models for the galaxies and intercluster baryons, we will produce galaxy-shear lensing predictions and strong lensing statistics for surveys such as Euclid. These results will be presented in a series of companion papers.
Mock catalogues constructed using three semi-analytical models, ν2GC (Makiya et al. 2016; Shirakata et al. 2019), SAG (Cora et al. 2018), and SAGE (Croton et al. 2016) will be released as DR2 in the near future. All data will be made publicly available on http://skiesanduniverses.org/.
ACKNOWLEDGEMENTS
The authors wish to acknowledge the referee of this paper, Chris Power, for his valuable comments. We thank the Instituto de Astrofísica de Andalucía (IAA-CSIC), Centro de Supercomputaciń de Galicia (CESGA, https://www.cesga.es), and the Spanish academic and research network (RedIRIS, http://www.rediris.es) in Spain for hosting Uchuu DR1 in the Skies & Universes site (http://skiesanduniverses.org/) for cosmological simulations. We are specially grateful to Antonio Fuentes, and his team at RedIRIS, for providing the skun@IAA_RedIRIS server that hosts Uchuu DR1 through Skies & Universes with a fast download speed trough their RedIRIS High Speed Data Transfer Service; to Javier Cacheiro, Carlos Fernández, Ignacio López, and Pablo Rey at CESGA for developing the Uchuu-BigData platform and providing the computer resources; and the staff at the IAA-CSIC computer department for proving support and managing the skun@IAA_RedIRIS server.
We thank Kazuki Kinjo for helping to construct the Uchuu merger trees. We are grateful to our Uchuu Collaborators Ángeles Moliné, Miguel Sánchez-Conde, and Alejandra Aguirre-Santaella for sharing preliminary results of their ongoing study on the properties of Uchuu subhaloes, which served as a helpful sanity check to some of our results. Their subhalo work, that will include full details on Uchuu subhalo abundances, distributions, and concentrations, will be published in a forthcoming publication. We also acknowledge Chi An Dong-Páez, IAA Summer-2020 student, for developing the Jupyter notebook Playing with Uchuu on your own computer, and helping to test Spark notebooks on the Uchuu-BigData@CESGA. We would like to thank Britton Smith for quickly adding the capability to load the new merger tree format into ytree (Smith & Lang 2019).
The Uchuu simulations were carried out on Aterui II supercomputer at Center for Computational Astrophysics, CfCA, of National Astronomical Observatory of Japan, and the K computer at the RIKEN Advanced Institute for Computational Science (Proposal numbers hp180180, hp190161). The Uchuu DR1 effort has made use of the skun6@IAA facility managed by the IAA-CSIC in Spain, this equipment was funded by the Spanish MICINN EU-FEDER infrastructure grant EQC2018-004366-P. The skun@IAA_RedIRIS server was funded by the MICINN grant AYA2014-60641-C2-1-P. The numerical analysis was partially carried out on XC40 at the Yukawa Institute Computer Facility in Kyoto University.
TI has been supported by MEXT via the ‘Priority Issue on Post-K computer’ (Elucidation of the Fundamental Laws and Evolution of the Universe), JICFUS, and MEXT via the ‘Program for Promoting Researches on the Supercomputer Fugaku’ (Toward a unified view of the universe: from large scale structures to planets, proposal numbers hp200124). TI thanks the support by MEXT/JSPS KAKENHI Grant Numbers JP17H04828, JP18H04337, JP19KK0344, and JP20H05245. FP, AK, and DM thank the support of the Spanish Ministry of Science and Innovation funding grant PGC2018-101931-B-I00. Parts of this research were conducted under the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. EJ acknowledges financial support from CNRS. FP and EJ want to thank a French–Spanish international collaboration grant from CNRS and CSIC. CVM acknowledges support from FONDECYT through grant 3200918, and he also acknowledges previous support from the Max Planck Society through a Partner Group grant. SAC acknowledges funding from Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET, PIP-0387), Agencia Nacional de Promoción de la Investigación, el Desarrollo Tecnológico y la Innovación (Agencia I+D+i, PICT-2018-03743), and Universidad Nacional de La Plata (G11-150), Argentina.
Numerical analysis were partially carried out using the following packages: numpy (van der Walt, Colbert & Varoquaux 2011), scipy (Virtanen et al. 2020), h5py(Collette 2013), matplotlib (Hunter 2007), colossus (Diemer 2018), and ytree (Smith & Lang 2019). We thank the developer of colossus, Benedikt Diemer, for implementing the mass–concentration relation of this paper in colossus.
DATA AVAILABILITY
As DR1, we release various N-body products for the Uchuu suite on http://skiesanduniverses.org/, such as subsets of simulation particles, matter power spectra, halo/subhalo catalogues, and their merger trees. Non-public data are available upon request. Under the UchuuProject on Github,13 we provide a collection of general tools for the community, codes/scripts/tutorials and Jupyter notebooks for the analysis of the Uchuu data.
Footnotes
Uchuu means ‘Universe’ in Japanese.
Shin means ‘deep’ in Japanese.
REFERENCES
APPENDIX A: HOW ACCURATE ARE ESTIMATES OF HALO CONCENTRATION?
Here, we investigate the accuracy of our methods to estimate halo concentration. We start with random realizations of dark matter haloes having either NFW or Einasto density profiles. We then proceed by measuring concentrations using averaged halo profiles from the Uchuu simulation at z = 0 and z = 1.4. These results are compared between the Uchuu, Shin-Uchuu, and Phi-4096 simulations, each having significantly different mass resolution.
A1 Random realizations of NFW haloes
This is a simple test: make a random realization of an NFW halo with a given concentration and some number of particles. Because, by design, the concentration Ctrue is known, ideally the algorithm should find it. However, there is always noise in any such measurement due to the finite number of particles, and the algorithm may produce biased estimates.
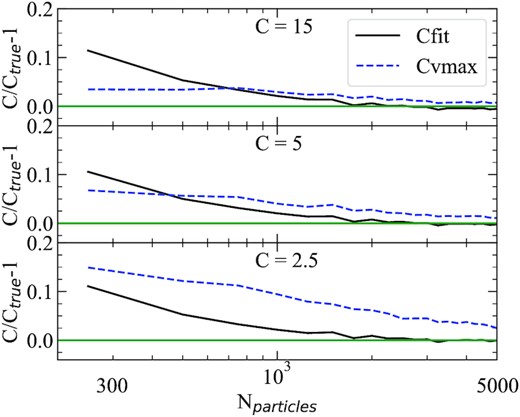
We approximately follow the procedure used by the rockstar halo finder (Behroozi et al. 2013a). All particles are sorted by distance. Binning is done by constant mass so that each interval has the same number of particles (S/N). The total number of bins is 50. However, the first bin is special: it always has 15 particles. We then measure the density and circular velocity for each bin. A density profile is then fitted using the NFW profile, providing a concentration value Cfit. Similarly, a circular velocity curve is used to find Vmax, leading to an estimate of a concentration value Cvmax. Many realizations (typically 300) are performed to find the average and rms measurement of each true concentration.
Fig. A1 presents C/Ctrue as a function of particle number for each method. The three panels show three selected values for the true concentration: Ctrue = 15 for high concentration haloes like our Milky Way, Ctrue = 5 for intermediate haloes, and Ctrue = 2.5 for very low concentrations, close to the minimum concentration of the simulations at high redshifts. The deviation from the true value is found to depend on the number of particles Nparticles, the input concentration Ctrue, and the method used. For very small particle number (Nparticles ≲ 500), the Vmax method provides more accurate results. For large particle number (Nparticles ≳ 3000), fitting the density profile gives better results. However, the differences are small for concentrations C ≳ 3, and less than ∼2 per cent for Ctrue > 5 and Nparticles > 3000. The only substantial errors happen at very low concentration where Cmax can be systematically above the true values by 10–15 per cent. The main reason for this is related to the fact that the radius corresponding to Vmax is very close to the radius of the halo, and fluctuations are amplified producing an upward biased estimate.
Accuracy of recovering the concentration for haloes with random realizations of the NFW density profile. The difference between the measured and true concentration is dependent on the number of halo particles Nparticles, the input concentration Ctrue, and the measurement method. For very small number of particles (Nparticles ≲ 500), the Vmax method provides more accurate results. For a large number of particles (Nparticles ≳ 3000), fitting the density profile gives better results. Overall the differences are small for concentration C ≳ 3, and less than ∼2 per cent for Ctrue > 5 and Nparticles > 3000.
The main take away of this test is that both methods produce nearly the same estimates of the true concentration if the density profile is NFW and the number of particles is more than 3000.
A2 Random realizations of Einasto haloes
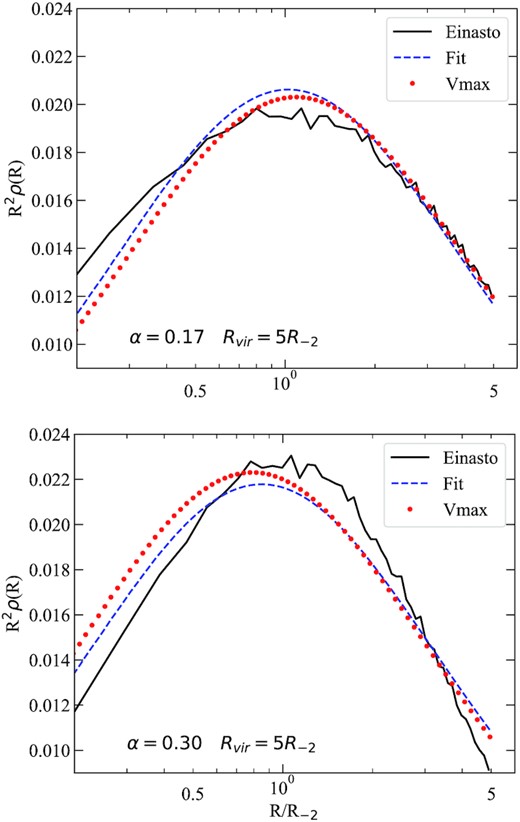
Fig. A2 gives the example of two Einasto profiles with different shape parameters. In the top panel, we show α = 0.17, which is typical for galaxy-sized haloes. Such haloes have a relatively broad profile and are reasonably accurately fitted by the NFW profile. In the bottom panel, we show α = 0.30, which is more characteristic of massive clusters or, in general, for high peaks in the initial density field. Because the shape of such haloes are not NFW, there is no true concentration using the formal definitions. However, we can still apply our methods and see how accurately the density profile is described.
Two examples of fitting Einasto profiles with the NFW profile and using two methods to measure the concentration. Parameters of the Einasto profile are indicated in the panels. For both cases, a halo single realization with 300 000 particles was used. The profile in the top panel has a shape parameter α = 0.17 that can be reasonably well approximated by the NFW profile for radii R ≳ 0.1Rvir. Indeed, the error in density at those distances are less than ∼5 per cent. Both methods provide similar quality fits. The bottom panel shows the case of large shape parameter, α = 0.3, which is typical for very massive haloes that form in high ν = δc/σ(M) ≈ 4 density peaks. The Vmax method provides a better approximation for the outer region R > 0.1Rvir, while the direct fitting method is slightly better in the centre. In both cases, the error on the density is ∼10 per cent for R > 0.1Rvir. Density is shown in arbitrary units.
Not surprisingly, fits for α = 0.17, while not perfect, are relatively good. The errors where the density profile peaks (at 1/5 the halo radius) are approximately 5 per cent and increase towards very small radii. The two methods of measuring concentration produce different estimates at the 20 per cent level. However, it is not clear which one is better overall. We find the Vmax method provides a slightly improved fit in the outer regions of the halo, while the fitting method is better towards the halo centre.
The α = 0.30 halo is much more difficult to compare because the halo profile is far from NFW. The methods produce different concentrations, with Vmax predicting higher concentration and smaller errors in the outer regions.
A3 Average profiles of massive haloes in the Uchuu simulation
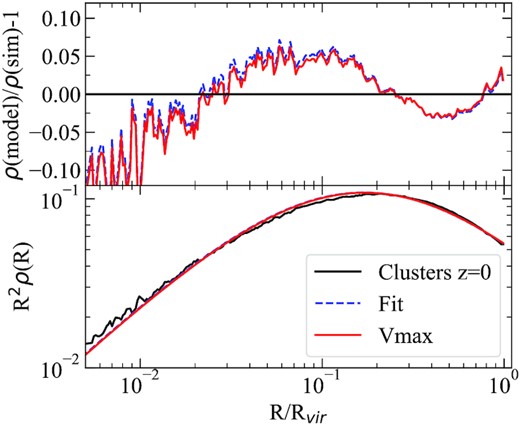
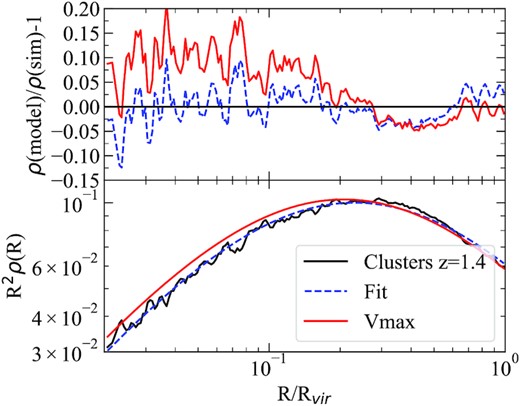
Here, we extend the above analysis to real haloes, and measure concentrations using the averaged profiles of massive relaxed haloes selected from a narrow mass interval. We define a halo to be relaxed if its offset parameter (the distance between the halo centre and halo centre of mass, measured in units of the virial radius) is less than 0.05, and its spin parameter less than 0.03. This is done to remove haloes that experience significant non-equilibrium events. Averaging over many haloes of the same mass serves the same purpose as smoothing substructures. Results are presented in Figs A3 and A4 for 100 clusters at z = 0 and z = 1.4, respectively.
Fitting the halo density profile of Mvir = 1.5 × 1015|$\, h^{-1}\, \rm M_{\odot }$| haloes at z = 0 with the NFW profile. The true halo profile was obtained by averaging the profiles of 100 haloes of this mass in the Uchuu simulation. Both halo concentration measurement methods provide nearly identical fits, with a ∼5 per cent accuracy for R = (0.01–1)Rvir. The lower panel shows R2ρ(R) in arbitrary units.
Fitting the halo profile of Mvir = 1.5 × 1014|$\, h^{-1}\, \rm M_{\odot }$| haloes at z = 1.4 with the NFW profile. The true halo profile was obtained by averaging the profiles of 100 haloes of this mass in the Uchuu simulation. Both halo concentration measurement methods provide nearly identical fits in the outer halo region R = (0.2–1)Rvir, accurate to ∼5 per cent, while the fitting procedure does better in the centre. The lower panel shows R2ρ(R) in arbitrary units.
At z = 0 both methods of measuring concentration produced very close estimates. Note that the halo profile we find itself is not an NFW; there are ∼5 per cent systematic deviations. The errors and the shape of the average halo profile are different at z = 1.4 compared with z = 0. Here, the fitting method works better except at the very outer 20 per cent region near the virial radius. The difference in concentration produced by the two methods is about 10 per cent, with the Vmax method predicting higher concentration.
A4 The convergence of halo concentrations
Because we have three simulations with vastly different force and mass resolutions, we can compare estimates of haloes concentration for haloes of the same mass found in different simulations. We can also investigate the minimum number of particles per halo that is required to determine the halo concentration robustly.
Fig. A5 shows the relative residuals of median concentration between the Uchuu and the Shin-Uchuu simulations as a function of halo mass. The difference is less than around 5 per cent for haloes more massive than ∼1012|$\, h^{-1}\, \rm M_{\odot }$|, corresponding to 3000 particles in the Uchuu simulation. For less massive haloes, the difference increases regardless of the halo mass. Therefore, we conclude that 3000 particles per halo is the minimum threshold for the Uchuu simulation to robustly measure concentration.
Relative residuals of the median values of halo concentration c200, comparing the Shin-Uchuu (higher resolution) and Uchuu (lower resolution) simulations, at z = 0.0, 1.0, 3.0, and 7.0. Concentrations are measured using the Vmax method. The vertical dotted line corresponds to a halo mass with 3000 particles in the Uchuu simulation. At this point, residuals become larger with decreasing halo mass.
Fig. A6 shows the relative residuals of median concentration between the Shin-Uchuu and the Phi-4096 simulations as the function of halo mass. Differences can be seen to increase systematically below ∼9.0 × 108|$\, h^{-1}\, \rm M_{\odot }$|, corresponding to 1000 particles in the Shin-Uchuu simulation. For more massive haloes, the difference is less than 5 per cent, except at z = 9.5 where the scatter is large due to poor statistics in the Phi-4096 simulation. However, we observe no systematic trend. Therefore, we consider 1000 particles per halo is the minimum threshold for the Shin-Uchuu simulation to robustly measure concentration. This value is smaller than that for the Uchuu simulation, reflecting that the softening length of Shin-Uchuu is much smaller. We also use this threshold for the Phi-4096 simulation because the ratio of mean particle separation to softening length is close to that of the Shin-Uchuu simulation.
Relative residuals of the median values halo concentrations c200, comparing the Phi-4096 (higher resolution) and Shin-Uchuu (lower resolution) simulations, at z = 7.8, 8.6, 9.5, and 10.5. Concentrations are measured using the Vmax method. The vertical dotted lines correspond to a halo mass with 1000 and 3000 particles in the Shin-Uchuu simulation.
APPENDIX B: ANALYTICAL MODEL OF MASS–CONCENTRATION RELATION
APPENDIX C: MASS–CONCENTRATION RELATION FOR RELAXED HALOES AND FOR OVERDENSITY 500 HALO DEFINITION
Fig. C1 shows the mass–concentration relation of the Uchuu and Shin-Uchuu simulations and their redshift evolution for only relaxed haloes. The concentrations are estimated using the Vmax method (equation 1). Overall trend is the same as the relation for all haloes (Fig. 9). The concentration for relaxed haloes shows a well-known behaviour that relaxed haloes have larger concentrations. Even for relaxed haloes, we observe a flattening and an upturn with increasing mass, consistent with Klypin et al. (2016). Fig. C2 also shows the mass–concentration relation, where concentrations are estimated by the profile fitting. The plot shows that the main tendencies of the concentration–mass relations do not depend on the method to find concentration. This includes the upturn in the concentration at large masses.
Concentrations for relaxed haloes using Vmax method (equation 1). Top panel: Mass–concentration relation of relaxed haloes for the Uchuu (thick curves) and the Shin-Uchuu (thin curves) simulations. The dashed curves are predictions of the analytical model described by equation (2). Bottom panel: The fractional difference between the halo concentrations of the Uchuu (squares) and the Shin-Uchuu (circles) simulations and the model predictions.
The same as in Fig. C1 but for concentrations estimated by profile fitting.
Bottom panels of Figs C1 and C2 show residuals of concentrations from the model. The accuracy level is similar to those for all haloes (Figs 9 and 10). We also confirm that the accuracy level is also comparable at mass M200 < 1011|$\, h^{-1}\, \rm M_{\odot }$| and redshift z > 7. We also provide best-fitting parameters of the mass–concentration relation with c500 estimated by profile fitting in Table 2 and show the result in Fig. C3.
Evolution of concentration–mass relation for all haloes. Concentrations are estimated by profile fitting and for the halo mass and concentration defined using r500, in which the average spherical overdensity is 500 times the critical density. Labelling of curves is the same as in Fig. C1.
APPENDIX D: VALIDATION OF MERGER TREES
Our use of consistent trees needed to be modified to make merger tree construction possible on simulations of the size of those in the Uchuu suite. As explained in Section 2, to overcome this hurdle, we split the full box of each simulation into smaller regularly spaced subvolumes, and ran consistent trees for each subvolume separately. In this section, we compare merger trees of the mini-Uchuu simulation constructed by this method and the original consistent trees code in order to show the robustness of this method.
A number of metrics have been used to evaluate merger trees such as length of tree and mass growth history of haloes (e.g. Srisawat et al. 2013), and merger rate. Visualization tools have also been provided (e.g. Poulton et al. 2018; Smith & Lang 2019). Here, we use mean merger rate because mergers trigger a number of events in semi-analytical galaxy models. Given a halo with mass Mi at redshift zi, we define the merger mass ratio ξ = Mi − 1,j/Mi − 1,0, where i and j denote the snapshot id and progenitors of the halo, respectively. We set the progenitor with j = 0 to be the most massive progenitor and compute the number of mergers per halo as a function of zi, ξ and the descendant halo mass Mi.
Fig. D1 shows the comparison of mean merger rate of trees of the mini-Uchuu simulation constructed by our method (|$\langle N^{\rm para}_{\rm merger} \rangle$|) and the original consistent trees code (|$\langle N^{\rm std}_{\rm merger} \rangle$|) as a function of redshift for three halo mass bin and three merger mass ratio. Except for the most massive halo mass (1014–14.25|$\, h^{-1}\, \rm M_{\odot }$|), the difference of both methods is always within 5 per cent, ensuring the accuracy of our method. For haloes with 1014–14.25|$\, h^{-1}\, \rm M_{\odot }$|, both merger rates converge well within 5 per cent level with little exceptions. There are four spots for ξ > 10−1 and one spot for ξ > 10−2, where the difference exceeds 10 per cent. This is because such mergers with massive haloes are rare and the number difference at each redshift is only one. Thus, this large difference in ratio is not significant.
Comparison of mean merger rate of trees of the mini-Uchuu simulation constructed by our method (|$\langle N^{\rm para}_{\rm merger} \rangle$|) described in Section 2 and the original consistent trees code (|$\langle N^{\rm std}_{\rm merger} \rangle$|) as a function of redshift for three halo mass ranges, and three merger mass ratios ξ.
We also perform a stricter test. Fig. D2 shows the comparison of the total number of progenitor haloes and subhaloes of the tree of the largest halo (∼2.0 × 1015|$\, h^{-1}\, \rm M_{\odot }$|) at z = 0 in the mini-Uchuu simulation as a function of redshift for four progenitor mass ranges. The number of progenitors agrees well with each other for progenitor mass more massive than 1012|$\, h^{-1}\, \rm M_{\odot }$|. For less massive progenitors there are small deviations, but which are typically only less than 5 per cent level. We conclude that merger trees constructed by our method are equivalent to those obtained from the original consistent trees code.
Total number of progenitor haloes and subhaloes Nprog of the tree of the largest halo at z = 0 in the mini-Uchuu simulation as a function of redshift for four progenitor mass ranges. Symbols denote results of our method, and solid curves denote those of the original consistent trees code.